Reason 1: Reclaimed Class time
Metric-only STEM instruction would allow educators to reclaim the copious amount of instruction time spent on teaching definitions of, and the forced relationships between, customary units.
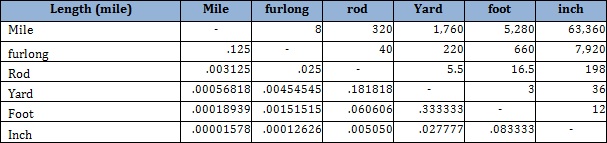
Customary units are NOT a system of measurement. A system is a set of interconnecting parts forming a complex whole. Customary units are an assortment of disparate, unconnected units based on historical artifacts and colonial legacies chiefly supported through our continued teaching of them and reinforced by our consumption habits. In the classroom, this fact translates into copious amounts of instruction time. As there is no consistent relationships in customary units, no knowledge is transferable. A student could master the measure for length but that will not facilitate learning in any other measure. Students must start from the beginning with each new measure. Furthermore, the inherent difficulties of working with customary units absorb significant class time, even when teaching and learning basic concepts. This is so because customary units require complex multiplication and division earlier and more frequently than metric units. With customary units, students often focus on the convoluted process needed to solve a problem without ever understanding the concept in which the problem was intended to teach.
US Customary Units:
In contrast to customary units, the modern metric system is indeed a true system. In the classroom, once a student masters the units within one measure, such as length, they immediately understand the unit relationships throughout the entire metric system. All knowledge gained is transferable in every other metric measure and throughout every classroom lesson.
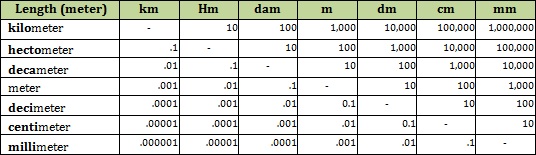
Metric Units:
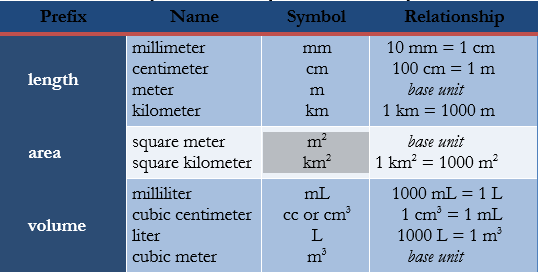
Another benefit is that the metric system is a base ten system. This simply means that unit conversions are always by 10. Prefixes like centi-, kilo-, and giga- are used throughout the system to indicate magnitude of the unit. For instance, a kilometer is ten times (103) the distance of a meter. The beauty of metric system nomenclature is that students only have to look at the unit name to know the quantity it represents; customary units required all memorization. Furthermore, in the metric system a student can convert measurement units quickly and accurately by simply moving the decimal point the correct number of places in either direction. Understanding factors, the ability to easily scale up or scale down quantities, and simplified mathematical calculations are important tools for conducting, designing and comprehending scientific studies.
How does the chosen units of measurement impact teaching and student learning?
The concept of volume is just one example of how metric units facilitate easier teaching while increasing student learning in fundamental mathematical concepts. The Common Core Standards in Mathematics introduce cubic units in Grade 5 in Standards 5.MD.C3-5. One reason volume has been so difficult to teach in earlier grades is the lack of a relationship between units. In U.S. customary units, for example, we measure length in inches (or yards), but we cannot cube an inch (or foot) to derive ounces, quarts, or gallons. To complicate things more, customary units even require different calculations for dry volume measures and wet volume measures, such as dry and wet pints.
In great contrast, metric units move gracefully from length, to area, to dry volume, and finally to liquid volume. Metric units and measures were designed to be related; these connections make understanding spatial measurement, the preferred U.S method for teaching measurement, easier to comprehend and easier to extrapolate.
Putting Base-10 in the Hands of Babes
In the picture below which features common elementary school level manipulatives, let’s say 1 golden bead equals 1 centimeter. Children who can count to ten can clearly see that 10 x 10 equals a square of 100 cm (beads), then they can see that 10x10x10 (cm3) equals a cube of 1000 cm. Volume and the relationships among length, area, and volume suddenly become intuitive in a base 10 system. Base ten is considered the best practice internationally for learning numbers and operations. The new Common Core Standards in Mathematics should be applauded for its focus on Base Ten learning in Numbers and Operations. Base ten educational practices coupled with metric-only measurement instruction would allow Educators to create synergy among the mathematical concepts of numbers, operations, and measurement.
Additional ways to understand the relationships among metric measures
Example 1: One millimeter (mm) of rain is one liter per square meter (L/m2). Imagine a 10 cm square block carved into 1 mm thick slices, you’d have 1,000 ten centimeter blocks which would make up a square centimeter. If you receive 10 mm of rain you have 10 L/m2. Stated another way, cubic centimeters (cc) ARE milliliters (ml)- 1,000 cc’s is 1,000 ml
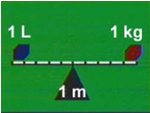
Example 2: You can also divide 1 meter by exactly 10 equal parts (10 cm x 10 cm x 10 cm), then make a cube (1,000 cm³) of it to fill with water, and you will find that it contains exactly, 1 L (1 liter) (1,000 mL) of water and is the mass of exactly 1 kg (1 kilogram) (1000 g). These measures are all related in base 10.
In conclusion, as a hodgepodge of units, customary unit teaching and learning translates into copious amounts of instruction time on unnecessary rote exercises. However, if we taught a metric-only measurement curriculum, many more children would accelerate into higher-level thinking skills. Not only would we simplify calculations but we could also create the foundation for scientific literacy easier and earlier. For instance, in Grade 8, the Common Core introduces scientific notation, a key skill to have for STEM education, although some groups, like the U.S. Coalition for World Class Math, argue this concept should be taught earlier. If we utilized the metric system, it would be possible to teach exponents and scientific notation in elementary school. By referencing to Table A above, we can see the the exponent of 10 (ie: 103 = 1000) corresponds exactly to the number of zeroes (or placeholders) in its numerical equivalent. Meaning, that metric system knowledge also transfers to the teaching and learning of exponents and scientific notation. Metric-only math and science instruction would allow our Educators to reclaim one of their more precious resources- class time!