“Civilization advances by extending the number of important operations which we can perform without thinking of them”- Alfred North Whitehead
What are the differences between customary units (inch-pound) and metric (meter-gram) units?
Customary units are NOT a system of measurement.
A system is a set of interconnecting parts forming a complex whole. Customary units are an assortment of disparate, unconnected units based on historical artifacts and colonial legacies chiefly supported through our continued teaching of them and reinforced by our consumption habits.
You’ll notice below that there are no consistent conversions between units (mile, foot) within a measure (length). Additionally, there are no connection points among measures (length and weight). Customary units do not even have primary definitions they are legally defined as fractions of metric standards.
In the classroom, this disconnect translates into copious amounts of instruction time. There are no consistent relationships in customary units; therefore, no knowledge is transferable. A student could master the measure for length but that will not facilitate learning in any other measure. Students must start from the beginning with each new measure. Furthermore, the inherent difficulties of working with customary units absorb significant class time, even when learning basic concepts. This is so because customary units require complex multiplication and division earlier and more frequently than metric units. With customary units, students often focus on the convoluted process needed to solve a problem without ever understanding the concept in which the problem was intended to teach.
Below are examples of the Customary measures for length and weight:
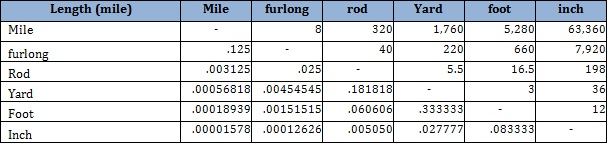

In contrast to customary units, the metric system is indeed a true system.
The units (centimeter, milligram) have simple and consistent meanings. The conversions are always by 10. The same six prefixes are used throughout the system to simplify the vocabulary. For each characteristic to be measured (except mass), only one unit is defined. That unit can then easily be scaled from very small to the very large by using one of the same six prefixes. The system allows unit conversions within all measures by merely moving the decimal point the correct number of places in either direction. In the classroom, once a student masters the units within one measure, they immediately understand the unit relationships throughout the entire metric system. Not only is class time regained through transferred metric unit knowledge but also class time is saved because metric computations are 44.9% faster and less error-prone. (Tew, 1985). Metric-only STEM instruction is the most beneficial and efficient use of limited class time.
All units of the metric system (except mass) have primary definitions based on scientific constants. For more than 200 years, the metric system has actively evolved by having scientific discoveries incorporated into its definitions. The metric system’s primary purpose is to facilitate easy mathematical and scientific calculations. The metric system allows a student to focus on the problem, not the process; thereby, freeing their brains for higher-order thinking.
Below are examples of two SI measures (base units) and the interrelationship between units:
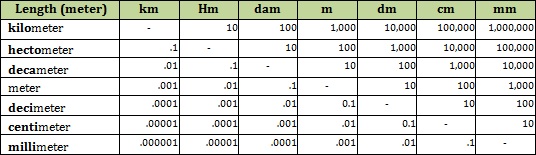

In the Metric System, not only were the units designed to be related but the measures themselves share science-based connections. These connections make understanding spatial measurement, the preferred method for teaching measurement, easier to comprehend and easier to extrapolate.
